社会経済研究所 コラム
2017年1月10日
2017年初のご挨拶、
読書日記（４）：
「孤高の数学者」岡潔と「発見の鋭い喜び」
新年を迎え、皆様にはお健やかにお過ごしのこととお慶び申し上げます。本年も社会経済研究所、本コラム並びにメルマガを、よろしくお引き立てのほどお願い申し上げます。
昨年10月に、JERA・垣見社長を当所横須賀地区にお迎えし、ご講演を戴きました。博識で知られる垣見様のご講演は様々な示唆が満載で、いろいろと刺激を頂戴しましたが、その中で「孤高の数学者」岡潔(1901-1978)について触れておられました。恥ずかしながら私は岡潔についてほとんど知らず、慌ててご紹介戴いた書籍（注1） を購入し、年末にかけて読み込んだ次第です。
岡の業績や人となりについては参考書籍に譲りますが、京都帝国大学を卒業後フランスに留学、帰国して後に大学の職を辞して郷里の和歌山県の山里に移り住み、市井の研究者として晴耕雨読の生活を送りながら、学術論文に加えて多くの随筆を執筆した、まことに希有な人物です。専門の数学の分野では、多変数解析関数論で世界的な業績を挙げた、とのことですが、もちろん私にはその内容や価値に言及する資格はありません。
書籍を通じて岡の思索に触れてみるに、私自身がそれを受け止める上で、数学の素養だけでなく、岡の語る俳句の解釈論に始まる人間訓に対する理解力の乏しさをも痛感させられました。ただ、その中で、岡が研究という行為において時として実感できる「発見の鋭い喜び」について語っている箇所は、強く印象に残りました。
私自身、このコラムで「研究という営み」について何度かお話ししていますが、岡の業績に比肩するものなど何一つない私でさえ、岡の言う「発見の鋭い喜び」（注2）に類するであろうものに触れる機会はままあるもの（注3）です。しかも、そのような体験は、再び同様の喜びを感じたいという、更なる研究に自らを駆り立てる意欲や熱意の源泉にもなっていきます。
私どもが携わる社会科学研究では、法・制度であれ経済であれ、あるいは哲学、倫理といった領域であれ、人間の行いが研究対象になりますので、「発見」ということはむしろ少なく、価値観に基づく比較衡量、すなわち「価値判断」が主たる作業です。
しかしそれでも、「発見の鋭い喜び」を感じる場面が無いわけではありません。現実に何が起こっているかを正確に読み解くこと、それが何に起因するかを正確に探り当てること、そしてどうすればそれを克服ないし改善できるかを編み出すことは、いずれも難しいことですが、苦労の末に辿りついた答えが美しく輝いて見えることがある（注4）のです。
本2017年も、そのような「発見の鋭い喜び」の瞬間に出会うこと、また後進の研究者たちにそのような瞬間を一つでも多く体感してもらうことを念願しつつ、精進して参りたいと存じます。益々のご指導、ご鞭撻のほど、よろしくお願い申し上げます。
- 注1：岡潔（森田真生編）「数学する人生」新潮社(2016)：森田真生「数学する身体」新潮社(2015)。なお、この2冊は主旨も趣もだいぶ異なるものです。前者は岡（一部ミチ夫人）の著作や講演原稿により、その人生行路とともに、人間としての心持ちのあり方に対する考え方や教訓を綴っています。後者は、原始的な算数（数のかぞえ方）から発展し、数学という理論体系を完成させる過程、さらには数学的処理を機械化することが、数学を人間から切り離すかのように見えるものの、実は人間の脳内過程や「心」を分析することに立ち返って行くという、壮大な「数学の進化論」が語られます。そして、後段1/3ほどの紙数を用いて、著者の森田氏がそのような数学的思索を歩むきっかけとして、岡の半生が綴られています。本コラムを読んでご興味を持たれた方もおられるかと思いますので、岡の人間訓に興味を惹かれた方は前者を、「数学」というものにより興味のある方は後者を、まずお手に取って戴き、さらにご興味あればいま一方に読み進む、という読み方をお勧めしておきます。
- 注2：岡自身の例示として、アルキメデスが入浴中に「比重」の原理を発見し、喜びの余り裸で戸外を走り回るという逸話が挙げられています。対して、岡の専門とする数学の偉大なる先達であるポアンカレの「証明の隅々まではっきりわかる」ことについては、余計なことであり「発見の鋭い喜び」が伴っていない、と論じています。ここで私が想起した例を並べるのもおこがましいと思いつつ、小学生の頃に読んだガリレオ・ガリレイの伝記に出てきた、ガリレオが幼少期に教師からの手ほどきを得た、地面に小石を並べて三角形や四角形を作る作業をご紹介させて下さい。参考図をご覧下さい。世に「天才」と称されるような科学者は、そのような「発見の鋭い喜び」を若年のうちに体感し、それを生涯かけて追い求めることで生まれるのではないかと想像するのです。
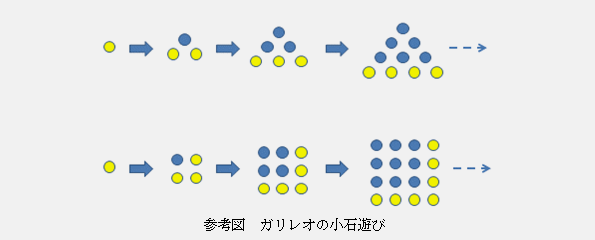まず、石を1つ置きます。三角形を作るためには、石を2個追加します。次にこれを大きくするには3個の石を、さらに大きくするには4個の石を…となります。四角形の場合は、最初の1つに3個を、次に5個を、さらに7個を…となります。幼いガリレオは（ついでに言えば、小学生の私も）、これで「数字の不思議」に開眼することになりました。
もちろん、ある程度数学を学んでしまえば、
- 三角形：n番目の三角形の個数（面積）はSn=n(1+n)/2であり、これは初項a1=1、交差d=1の等差数列の和に等しいので、n-1番目の個数との差は常にnである。
- 四角形：n番目の四角形の個数（面積）はSn=n^2であり、n-1番目の個数との差はn^2-(n-1)^2=2n-1となるので、常に「n番目の奇数」である。
- 注3：私自身の個人的経験、しかもかなり以前のことを申し上げるのは不遜なことですが、あえて例示させて戴きます。入所直後、私は原子燃料サイクルの数値モデル分析を手掛けていました。その中で、線形計画法を用いて総システム費用を最小化する最適解を導くモデルを開発し、いろいろ数値実験をしたのですが、入力した条件から特定の傾向の答えが当然出るはずだと予想して計算しても、全く違う方向の解が得られることがありました（当時私は、この現象を「鰻は予想外の隅に逃げる」と表現していました）。具体的には、使用済み核燃料再処理コストの低減は、積極的なPu（プルトニウム）利用への後押しとなり、具体的には高速増殖炉（FBR）導入を促進すると考えたのですが、実際に計算してみると必ずしもそうなるとは限らず、むしろ軽水炉でのPu燃料燃焼利用（いわゆる「プルサーマル」）、すなわち使用済み燃料処理対策の一部としての「消極的な消費」へ向かうことがあり得る、ということがわかりました。まあ、現在の条件下ではいろいろな意味で現実味を失ってしまったシミュレーション計算ではありますが、「最適化モデル」という手法の真髄の一端を垣間見たように感じたものです。もはや30年近く前の研究ですのでお勧めはしませんが、もしご興味を惹かれた方がおられましたら、一応ご参考まで出典を挙げておきます。
- 注4：これも手前味噌で恐縮ですが、私どもの2016年の成果からいくつかそのような例に触れてみたいと思います。まず、震災以降の各管内の電力需要がマクロ経済の回復ほどに戻らないという現象について、経済分析による接近を試みた結果、産業用需要では素材産業がリーマンショック前後で、素材産業では震災前後で、生産弾力性が変化したこと、家庭用需要では震災後の電気料金上昇に節電の定着が重畳したこと、を明らかにしました。もちろん、「いつ」「何が」起きたかの両方を同時に解明できたわけではなく、まだまだ分析不十分と評価される方もおられるかも知れません。ただ、いろいろな方からご要望を頂戴する中で、苦労して辿りついた解であり、私としても相応の愛着を感じている次第です。ご興味ある方は、以下を参照下さい。
また、2016年は再生可能エネルギー大量導入に伴う諸課題の分析と対応策の立案に、最も多くのエネルギーを注ぎました。具体的には「共食い効果（PVの大量導入が進むほど、自らの価値を低減させる現象）」「アデカシー確保の困難（（FIT等で支援された）安価な再生可能エネ電力が卸電力市場に投入されることで、既存のとりわけ調整用の火力電源が費用回収できず、退出を迫られる現象）」「デススパイラル（屋根設置型PV等の導入が電力需要の系統からの離脱を促し、配電部門の費用回収を困難にするが、料率を挙げることで回収しようとすればさらなる離脱を生じ、悪循環に陥る現象）」がその代表ですが、ドイツ等で既に生じているものもあれば、これから生じる可能性があるというものもあります。これらを総合的に分析し、対応策を見出すことは、同様の事情を抱える各国を見渡しても最先端の研究と言えるのではないかと思います。関連する報告書として、以下を挙げておきます。
