
電気新聞ゼミナール(269)
供給予備力の算定に必要な持続的需要変動はどのように試算されているのか?
長期での予備力
電力の安定供給のためには、供給エリア全体で十分な予備力の確保と、需給バランスの維持が必須である。長期計画において確保すべき供給力の考え方は、月次の最大3日平均電力(H3)を対象として、2つの要素から構成される。1つは偶発的需給変動と呼ばれ、気象の大幅な変動や発電所の計画外停止などによる需給変動に対応した予備力である。需給それぞれの確率分布に基づき算定され、H3の7%相当の確保が定められている。
もう1つは、持続的需要変動と呼ばれ、景気循環に伴う電力需要の変動に対応した予備力である。まず、気温補正済みH3実績を季節調整した上で、タイムトレンドへの回帰直線を計算し、そこからの乖離を算出する。これを景気に対応した変動とし、その最大値を持続的需要変動としている。これまでH3の1%相当とされ、偶発的需給変動と合計した8%を長期計画で必要な供給予備力としている。
しかし、この従来の手法では、持続的需要変動の評価が困難になっている。リーマン危機や東日本大震災を経て、電力需要のトレンドに変化が生じたことから、回帰直線の傾きや乖離が推定期間によって大きく変化してしまうためである。
状態空間モデルの活用
こうした問題に対し、電力広域的運営推進機関は状態空間モデルの活用に着目し、「調整力及び需給バランス評価等に関する委員会」の下に設置した「持続的需要変動に関する勉強会」において、その採否や運用について検討してきた。
状態空間モデルは観察できない時系列変数を推定する場合に有効なモデルであり、観測方程式と遷移方程式から構成される。持続的需要変動を推定するためには、気温補正済みH3が①トレンド成分、②循環成分、③季節成分の3成分に分解されることを示す観測方程式と、各成分の時系列構造が記述される遷移方程式から成るモデルが用いられる(図)。この場合、持続的需要変動は推定された②循環成分の最大値として計算される。
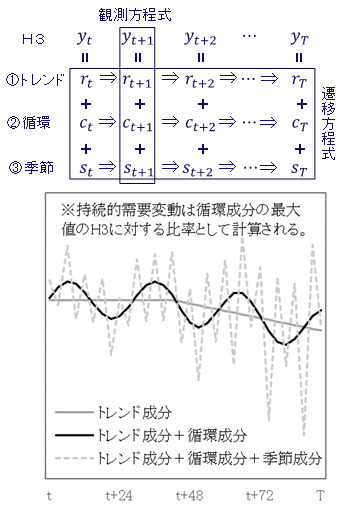
図:状態空間モデルによる持続的需要変動推定の概念図
注:状態空間モデルは、観察可能な変数を被説明変数とする観測方程式と観測できない変数の時系列構造を示す遷移方程式から成る。
22年9月に公表された勉強会報告書は、状態空間モデルによる推定結果を示しており、持続的需要変動のH3に対する比率(最大変動率)が、東日本大震災後の期間(12年4月~22年3月)では2.0%と、これまでの1.0%では供給力が不足する可能性を指摘している。また、当所が同報告書のために提供した、拡張型の状態空間モデル(※)による最大変動率の推定結果は、震災後期間で2.5%、リーマン危機や東日本大震災を含む96年以降の期間で2.8%であった。最大変動率の推定結果は拡張型モデルの方が大きいものの、推定期間の違いによる結果の変化は0.3ポイントと小幅に止まっており、既述の問題に応えた結果が得られている。
※誤差項の分布に、通常用いられる正規分布でなく、より裾の厚いt分布を適用したモデル
必要とされる頑健な推定
持続的需要変動の上昇は、供給信頼度を維持するために必要な供給予備力が増加することを意味する。容量市場においては、持続的需要変動が目標調達量を算定する諸元の一部となっており、その上昇は、同市場の需要曲線を右方向にシフトさせ、約定価格を押し上げることで、必要な電源投資を促すことが期待される。実際にこうした影響を与えうるという観点から、持続的需要変動の推定にあたっては、今後も慎重な検討を進めていく必要がある。
電気新聞 2022年10月12日掲載


